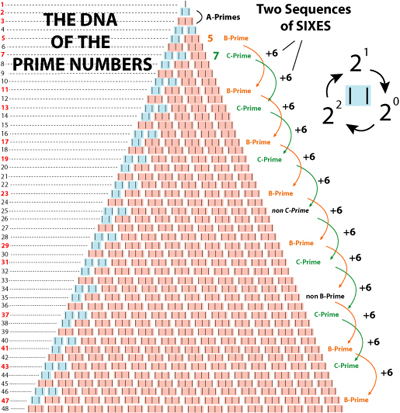
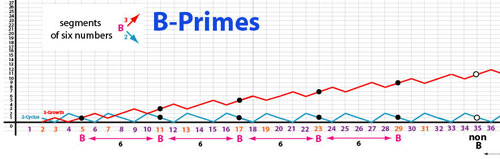
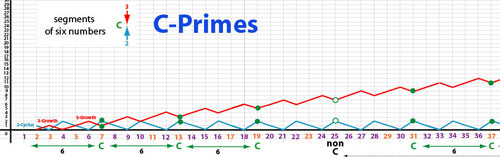
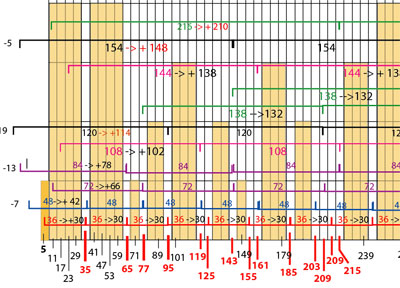
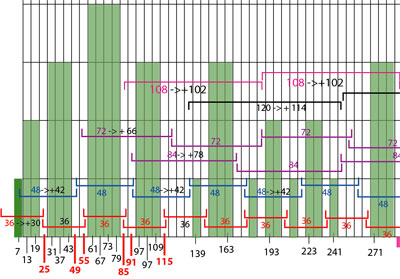
| De DNA van de priemgetallen Sedert 2000 jaar zoekt men naar wat priemgetallen eigenlijk zijn. Men gaat er steeds van uit dat het één reeks van unieke getallen is waarbij elk priemgetal enkel deelbaar is door zichzelf en door 1. Dat is juist, maar ... het is niet slechts één reeks. Het zijn in werkelijkheid twee - quasi parallele - reeksen van getallen. Wij kunnen dus van een soort DNA spreken. Op elke reeks liggen SPECIFIEKE priemgetallen. Eén van die reeksen begint van het getal 5, en de andere begint van het getal 7. Vanuit 5 én 7 worden dan steeds cycli van 6 bijgevoegd, dus steeds een opbouw met zes nieuwe eenheden. TWEE REEKSEN (de B-reeks en d C-reeks) Ik noem de reeks die met 5 begint de B-reeks. De B-priemgetallen liggen op een reeks die begint bij 5 en vervolgens wordt er sedert 6 bijgeteld. Dat geeft: 5, 11, 17, 23, 29, 35, 41, 47, 53, 59, 65, 71, ... Deze samengestelde nummers kunnen eruit gehaald worden via een reeks eenvoudige berekeningen, bv. voor de B-reeks : 5 + 30 + 30 + 30 + 30 + ... enz, , 11 + 66 + 66 + 66 + enz, 35 + 42 + 42 + 42 + enz. , 65 + 78 + 78 + 78 + ... enz. Voor de C-reeks zijn de "eliminatie reeksen" bijna hetzelfde, bv. 25 + 30 + 30 + 30 + ..., 7 + 42 + 42 + 42 + ..., 55 + 66 + 66 + 66 + 66 + ..., 85 + 102 + 102 + 102 + ... Deze eliminatie reeksen geven "samengestelde getallen", dus geen priemgetallen. De eliminatie-reeksen worden dan afgetrokken van de B en C-reeksen, en zo blijven enkel de echte priemgetallen over. Onze hypothese is dat zulke eliminatie reeksen continu blijven. Wellicht kunnen er wel unieke nieuwe combinaties gevormd worden, maar dat moet via sterke computers gecontroleerd worden. Bv. bij nieuwe priemgetallen die tijdens de opbouw worden gecreeërd. Met het relatief sterke computerprogramma Mathematica hebben wij onze stelling reeds berekend, en geen fouten gevonden. Duimen dus! ;-) Wel, als wij getallen als louter tweeën en drieën bekijken zien wij dat ALLE getallen met 2-en en/of 3-en kunnen beschreven worden. Dit is wellicht tegen onze dagdagelijkse logika maar toch kan men het ook zo bekijken. Hierna ziet U een driehoek (ongeveer de Driehoek van Pascal) die louter uit enen (I, II, III, IIII, ...) bestaat. De blauwe zones vormen een twee (2) en de rode zones een drie (3). Wij zien dat er weinig tweeën voorkomen, en zien zelfs dat er een cyclische beweging inzit bij de (blauwe) twee. Ook zien wij dat de priemgetallen in twee reeksen van zessen verdeeld zijn. Er zijn dus twee verschillende reeksen waarin STEEDS priemgetallen voorkomen. (ps: alle getallen kunnen bv. ook louter met 2,3 en 4 worden opgebouwd maar wij verkiezen voor onze analyse enkel 2 en 3)
Op bepaalde punten zien wij dat er in deze cyclussen van zes GEEN priemgetal voorkomt. Dus moet daarvoor een logische reden zijn.
|
|||||||||||||
|
Uit bovenstaande blijkt duidelijk dat de reeks van priemgetallen in feite bestaat uit een dubbele reeks van getallen.
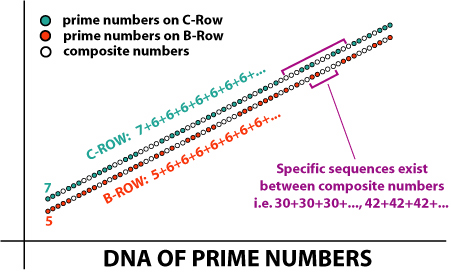 Deze twee reeksen zijn deel van zes reeksen. De vier andere reeksen D, E, F en G bevatten nooit priemgetallen, dit blijkt uit volgend overzicht. 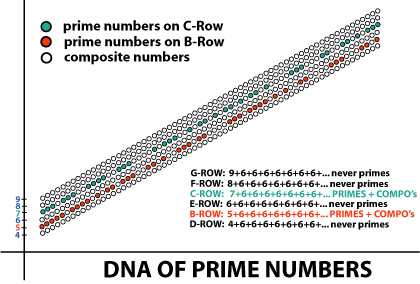 Dit is zichtbaar in volgende driehoek van tweeën en drieën. 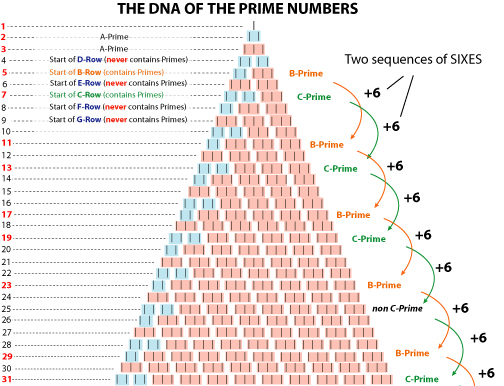
Indien U zelf de sekwenties willen nakijken download dan volgende pdf's van Mathematica. Eliminatie sekwenties van de B-reeks: (1), (2) Eliminatie sekwenties van de C-reeks: (1), (2) Auteur: © Dirk Laureyssens, 2006. All rights reserved. E-mail: dirk(at)mu6.com |
|||||||||||||
|
(credit Mathematica: Jan Devos/3ivx)
|