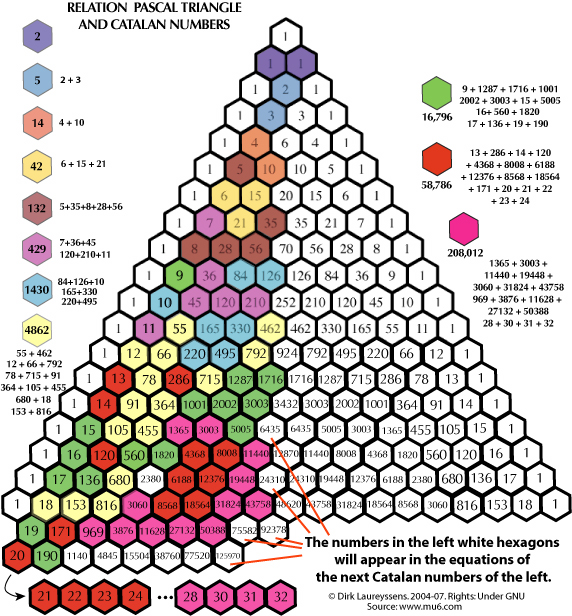
CATALAN NUMBERS.

You can see in next Pascal Triangle that each Catalan number is the sum of specific Pascal numbers.
The Catalan numbers occupy all Pascal numbers except the middle row and the rows of ones.
How can we interpret this strange finding? In our geometric/topogic approach of pelastration we have always unique combinations of space-time layers

In next image you see that on the fifth level there are 14 types of fives. The colors are just for clarity, but each combination of layers is unique.
In the above image you see that in the Pascal triangle the Catalan number 14 (orange) is composed by the Pascal number 4 + the Pascal number 10.
In the below image of Pelastratic layer combinations we see that we have 10 types composed by 4's and 1's [i.e. the first 5 is composed by a 4(+)+1], and 4 green types composed by 2's and 3's [i.e. the last 5 is composed by a 3(-)+2]. We can speak here almost of families of combinations. Thus the Pascal numbers indicate also the different types of Pelastratic combinations, and together some make a specific Catalan total.

Now the question remains how the distribution happens. I mean what is the systeem behind? Since the Pascal triangle has algebraic roots the amazing distribution of Pascal elements - which compose together specific Catalan numbers - has a mathematical logic which bring is a type a quality information. We can conclude that there is a system behind that brings us 'families' which make together a Catalan Tribe. I mean the Catalan number 58,786 (a tribe) is composed by 16 families (red hexgons) of sub-sets. The Catalan number 16,796 has 15 families (green hexagons). The Catalan number 4,862 has 15 families (light yellow hexagons). Etc.


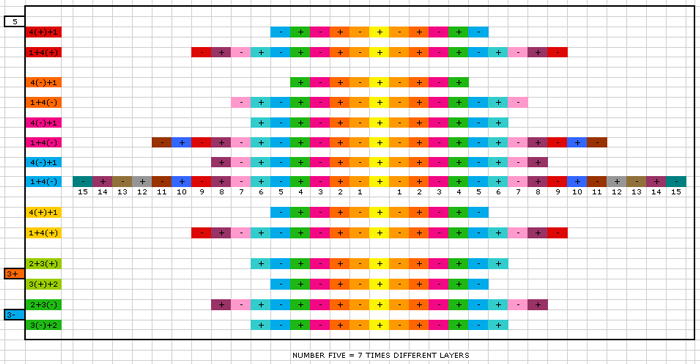
This image shows 14 geometric combinations of spacetime layers on the fifth level. There are 7 types qua number of layers (but each has another history). We can't just say that they are identical, even if the have an identical number of layers. For example the first 5 [4(+)+1] is not identical to the 12th 5 [3(+)+2] due the other parents, although both count 5 layers on each side.

Next image (click on to download the pdf) shows how the direction of a pelastration (membrane penetration) creates other membrane combinations in holons.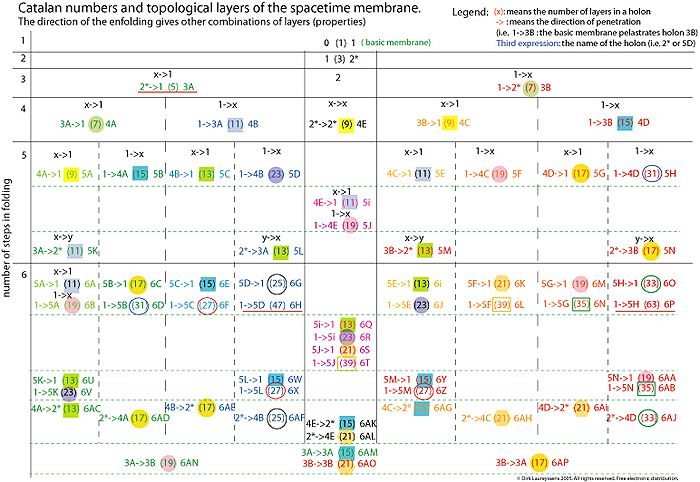
Next animated image shows in a dynamic way the first four steps of the growth of numbers (holons).

© Dirk Laureyssens, 2004. All rights reserved.